平衡树
搜索二叉树
概念
| 术语 | 说明 |
|---|---|
| 度 | 节点含有的子树的个数称为该节点的度 |
| 树的度 | 最大的节点度称为树的度 |
| 叶节点 | 度为零的节点 |
| 深度 | 对于任意节点 n，n 的深度为从根到 n 的唯一路径长，根的深度为 0 |
| 高度 | 对于任意节点 n，n 的高度为从 n 到一片树叶的最长路径长，所有树叶的高度为 0 |
| 森林 | 由 m（m>=0） 棵互不相交的树的集合称为森林 |
| 堂兄弟节点 | 同层的节点互为堂兄弟节点 |
| 兄弟节点 | 相同父节点的节点互称为兄弟节点 |
| 节点的祖先 | 从根到该节点所经分支上的所有节点 |
| 根据父节点被遍历输出的顺序 | 可以分为先序遍历,中序遍历,后序遍历。 |
| 红黑树的路径 | 从根节点到空节点被成为一条路径 |
二叉搜索（排序）树
构成条件:
若它的左子树不为空，则左子树上所有节点的值都小于根节点的值。
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值。
左右子树也分别为二叉搜索树。
性质
- 当在二叉搜索树当中搜索数据的时候，最多搜索高度次——O(n)，此时退化为单支，当二叉树平衡时，使用O(logn)时间。
注意
不允许存在重复节点。
在代码实现时，需要记录其父节点。
中序遍历有序，并且由于优先遍历当前最小节点，所以也是升序的。
删除节点
- 当需要删除的节点为
叶节点，直接删除即可。 - 当要删除的节点只有一个
子节点，将待删除节点替换为其子节点即可 - 当待删除节点的度为
2时：- 找到待删除节点在“中序遍历序列”中的下一个节点，记为 tmp 。
- 用 tmp 的值覆盖待删除节点的值，并在树中递归删除节点 tmp 即可——删除叶子节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53/* 删除节点 */
void remove(int num) {
// 若树为空，直接提前返回
if (root == nullptr)
return;
TreeNode *cur = root, *pre = nullptr;
// 循环查找，越过叶节点后跳出
while (cur != nullptr) {
// 找到待删除节点，跳出循环
if (cur->val == num)
break;
pre = cur;
// 待删除节点在 cur 的右子树中
if (cur->val < num)
cur = cur->right;
// 待删除节点在 cur 的左子树中
else
cur = cur->left;
}
// 若无待删除节点，则直接返回
if (cur == nullptr)
return;
// 子节点数量 = 0 or 1
if (cur->left == nullptr || cur->right == nullptr) {
// 当子节点数量 = 0 / 1 时， child = nullptr / 该子节点
TreeNode *child = cur->left != nullptr ? cur->left : cur->right;
// 删除节点 cur
if (cur != root) {
if (pre->left == cur)
pre->left = child;
else
pre->right = child;
} else {
// 若删除节点为根节点，则重新指定根节点
root = child;
}
// 释放内存
delete cur;
}
// 子节点数量 = 2
else {
// 获取中序遍历中 cur 的下一个节点
TreeNode *tmp = cur->right;
while (tmp->left != nullptr) {
tmp = tmp->left;
}
int tmpVal = tmp->val;
// 递归删除节点 tmp
remove(tmp->val);
// 用 tmp 覆盖 cur
cur->val = tmpVal;
}
}
AVL树(作者命名)
AVL 树既是二叉搜索树，也是平衡二叉树。
构成条件
- 它的左右子树都是AVL树。
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)，从而可以防止二叉搜索树的退化。
注意
- AVL 树的相关操作需要获取节点高度。
- “节点高度”是指从该节点到它的最远叶节点的距离。
- 叶节点的高度为
0，而而空节点的高度为-1。
平衡因子
节点平衡因子 = 左子树高度 - 右子树高度
对于一棵 AVL 树的任意节点的平衡因子始终保持在[-1,-1]区间。
AVL 树旋转
当平衡因子绝对值大于1时，对应的节点就被称为“失衡节点”。根据失衡情况的不同，又有不同的平衡方式:
左旋转：将失衡节点旋转到右子节点的左子节点位置。——LL
右旋转：将失衡节点旋转到左子节点的右子节点位置。——RR
对于左旋来说，如果它的右子树存在，那么:
右子树会代替失衡节点的位置，并且将失衡节点作为自身的左子树。
右子树本身的左子树，将会被嫁接到失衡节点的右子树位置。
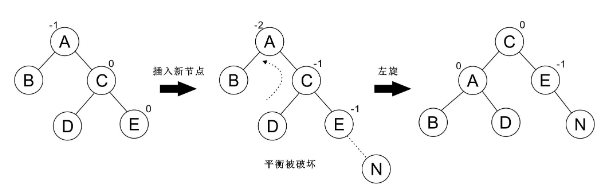
右旋则是以上操作的镜像
- 先左(右)旋后右(左)旋——LR(RL)
需要旋转两次，旋转方向和顺序与类型名称相同，也就是 LR 先左旋后右旋，RL 先右旋后左旋
步骤一：将新增节点的父节点，安插在根节点和根节点的左子节点之间。（谋权）
步骤二：然后将根节点变为它的空侧的子节点（篡位），然后将原新增的节点（就是被抛弃的子节点），变换原来的方向,嫁接在新根节点的子节点上（变节）
调整后的子树的根节点一定是新增节点的父节点，所以称之为谋权篡位
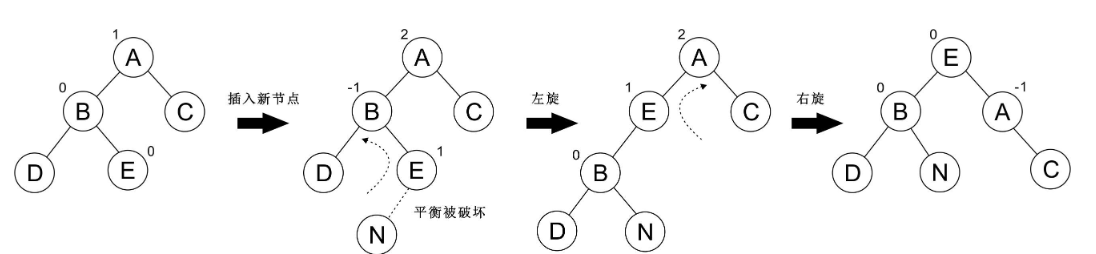
如何选择平衡？
LL：插入一个新节点到根节点的左子树（Left）的左子树（Left），导致根节点的平衡因子由 1 变为 2。
RR：插入一个新节点到根节点的右子树（Right）的右子树（Right），导致根节点的平衡因子由 -1 变为 -2。
LR：插入一个新节点到根节点的左子树（Left）的右子树（Right），导致根节点的平衡因子由 1 变为 2。
RL：插入一个新节点到根节点的右子树（Right）的左子树（Left），导致根节点的平衡因子由 -1 变为 -2。
例题验证
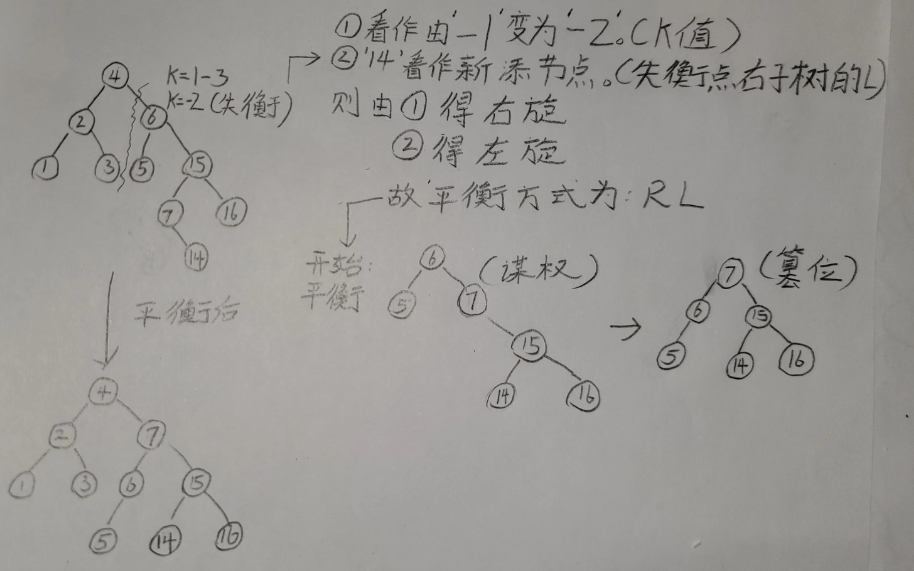
运用场景
由于AVL树需要旋转来保持平衡，而旋转是非常耗时的。因此：
- 适合用于插入 删除次数比较少，但查找多的情况。
红黑树(颜色命名)
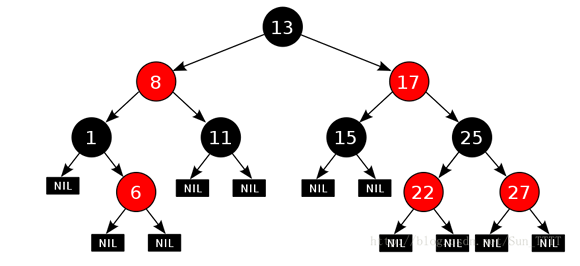
通过对任何一条从根到叶子的路径上各个节点着色的方式的限制。
性质
红黑树中，**
NIL节点（空叶子节点）为黑色**。节点为红色或黑色，且一个节点是红色的，那它的孩子必须是黑的。 —— 任何路径没有连续的红色节点。
根节点必须是黑色。
红黑树确保最长路径不会超过最短路径的两倍，且红黑树不是严格平衡。 —— 高效的关键。
每条路径，均包含相同数目的黑色节点。
任何不平衡都会在三次旋转之内调整完毕。
插入
插入
红色节点而不是黑色节点，因为插入黑色节点会影响性质 **5**，对其它路径产生影响。而且，如果当插入的节点的父节点是黑色的时候，那么就是完全正确的插入。但如果父节点是红色，那么会违反性质
2，此时要进行调整）。
如何平衡，旋转？详情——红黑树平衡变换
使用场景：
红黑树多用于搜索、插入、删除操作多的情况。